Procedural Generation
Fractal Noise
Fractals
Before we dive right into the application to noise, let's just briefly look at fractals, so we can define what 'fractal noise' is. Fractals are the result of repeatidly performing some action. The most famous examples are the Julia Sets and their map, the Mandelbrot Set. These are generated by taking a simple equation (on complex numbers), z <=> z^2 + c, and repeatidly feeding the output back into the function.
For these pure mathematical fractals, computers typically have a maximum number of iterations, and an 'escape' length for 'z' It applies the function to the starting point, and then feeds that number back into the function, until either:
- The maximum number of iterations has been reached.
- The 'length' of the complex number, z is greater than the 'escape' length.
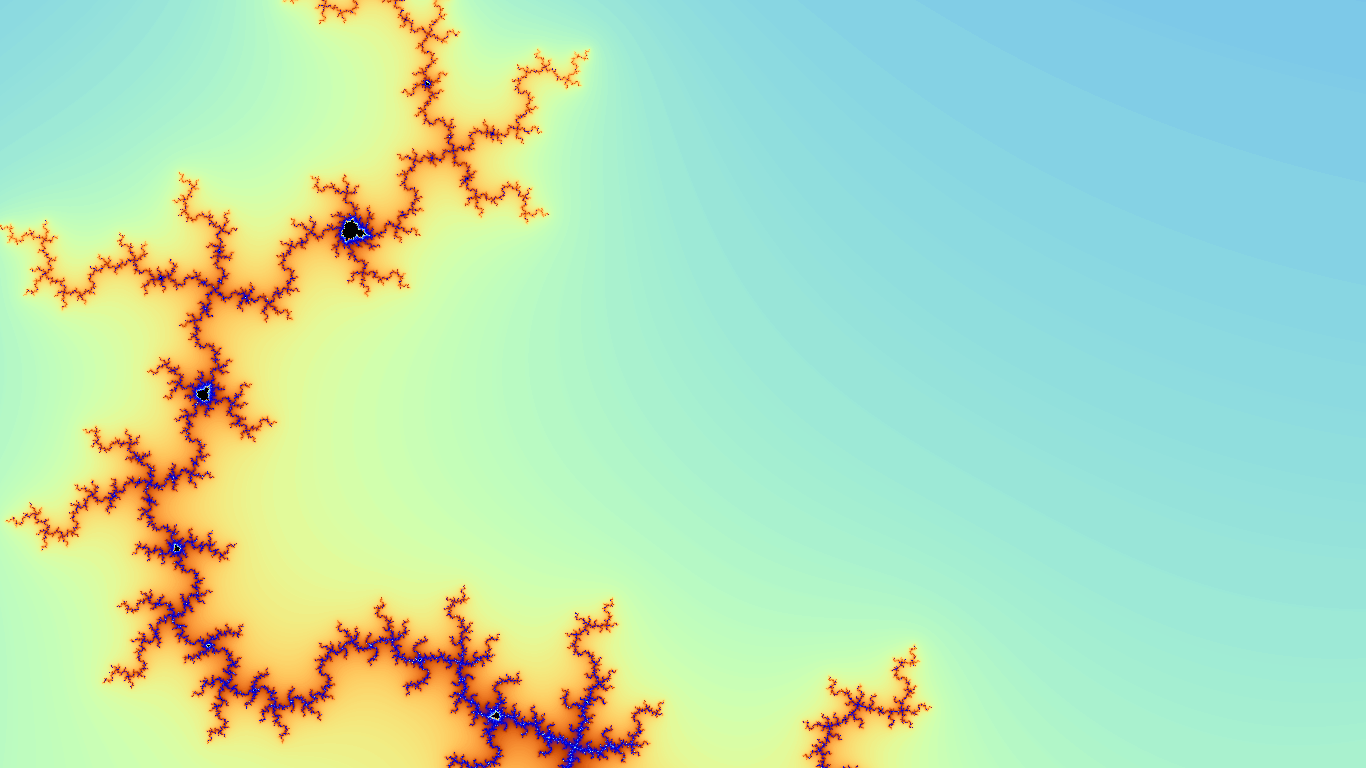
A subregion of the mandelbrot.

The full mandelbrot set.
The main point of fractals is that they are made by repeating the same process over and over. We can use the same idea to apply our noise function on itself, up to a number of times.
For the purposes of doing some neat stuff in the future, we'll be switching to a 3-dimensional version of our noise function. This function is also a bit more robust in terms of period, and more compact in definition.
float seed;
float hash(float n) { return frac(sin(n)*seed); }
float noise(float3 x) {
float3 p = floor(x);
float3 f = frac(x);
f = f*f*(3.0-2.0*f);
float n = p.x + p.y*157.0 + 113.0*p.z;
return lerp(lerp(lerp( hash(n+0.0), hash(n+1.0),f.x),
lerp( hash(n+157.0), hash(n+158.0),f.x),f.y),
lerp(lerp( hash(n+113.0), hash(n+114.0),f.x),
lerp( hash(n+270.0), hash(n+271.0),f.x),f.y),f.z);
}
Common 3d noise function found on
glslSandbox
and
shadertoy
adapted to Cg
This is a pretty interesting function, and is quite optimized. It has an inlined smoothstep applied on the fractional parts, and also fixes in the scales of the y and z axis at 157 and 113 (prime numbers). The mass of lerp calls below handle all of the interpolation needed, using the calculated 'smoothstep' values from the fractional parts. It also still has all of the properties we defined for coherent noise before.
Next, we must clarify what is meant by fractal noise, and have examples of how it is built. In the building of fractal noise, we use the basic noise function, and apply many octaves. The term 'Octave' is borrowed from music theory, as the typical application doubles the 'frequency' of the noise when moving from one octave to the next. Below are 6 live shaders, each rendering what one octave of noise looks like.
Octave 1
Octave 2
Octave 3
Octave 4
Octave 5
Octave 6
Combined wave
Each successive octave of noise is applied at twice the 'frequency' of the last. The 'period' of the noise is the distance between two 'samples', and just like with sound and music, the frequency is the inverse of the 'period'. However, in this case, the wave doesn't 'repeat' the same way. It still repeats, but over a much longer period, called the 'Tiling Period'.
The other measurement we make is the amplitude of each octave. This amplitude is reduced by a certain amount each octave, Called "Persistence". The higher this value, the more of the amplitude 'persists' per octave.
Below is the code used to generate a noised value in the range (0, 1) using the 3d noise function defined above.
//Defined externally from function
//so other parts of the program can modify
float scale;
float persistence;
int octaves;
float nnoise(float3 pos, float factor) {
float total = 0.0 //Total noise accumulated
, frequency = scale //Frequency of current octave
, amplitude = 1.0 //Amplitude of current octave
, maxAmplitude = 0.0;//Maximum for 'total'
//Accumulate noise over 'octaves' octaves
for (int i = 0; i < octaves; i++) {
//Apply a single sample of noise at a given amplitude
total += noise(pos * frequency) * amplitude;
//Move to next octave
frequency *= 2.0, maxAmplitude += amplitude;
amplitude *= persistence;
}
//Average expected value is half of maximum.
float avg = maxAmplitude * .5;
//Normalize the noise based on a 'factor'
//Factor value chooses how values are mapped to (0, 1)
// .5 maps values from .25 to .75 into the range (0, 1)
// .2 maps values from .4 to .6 into the range (0, 1)
//Values above or below the ranges all map to 0 or 1
if (factor > 0.0) {
float range = avg * clamp(factor, 0.0, 1.0);
float mmin = avg - range;
float mmax = avg + range;
float val = clamp(total, mmin, mmax);
return val = (val - mmin) / (mmax - mmin);
}
//Quickly handles full saturation (factor <= 0)
if (total > avg) { return 1.0; }
return 0.0;
}
//Default value used for factor, if not specified.
float nnoise(float3 pos) { return nnoise(pos, .5); }
Fractal noise using the same function defined further above.
The mapping between 0 and 1 is a very useful feature to have. When applying multiple octaves, the accumulated total gets higher and higher, and does eventually converge on some maximum value. However, for very high persistence (0.9-1.0), this maximum is very high. Additionally, for any persistence, the output values tend to cluster around the average (1/2 max). This makes unfiltered output very dull, with very little contrast. This normalization provides additional contrast, and standardizes the output of the function.
Even just using 1d noise, it is possible to apply the noise to create 'visual interest' in graphics. The following animation was made only noise based off of the x-coordinate of the screen.
Now, we can apply the same thing to 2d and 3d noises to create 2d and 3d fractal noises.
Octave 1
Octave 2
Octave 3
Octave 4
Octave 5
Octave 6
Combined noise
And then we can use this noise to produce textures. I took a look at a number of photoshop tutorials, and adapted them to run off the graphics card. This is one for camo. It's pretty simple: Apply multiple 'Difference clouds' on separate layers, then boost the contrast so there are only two colors (black/white). Remove one, and replace the other with the desired color. The below shader does the same thing, automatically, using the noise function! It can also be programmed to use different colors, and choose different cutoffs for choosing what color to use.
Next we will look at the process of developing textures using the noise functions. Continued on the Next Page.